Уважаемый аудио-энтузиаст,
На ваше рассмотрение представлен Muleteer DSP — модуль поддержания "быстроты" звучания. Этот DSP модуль разработан чтобы компенсировать избыточную массу звукоизлучающего прибора, и тем самым освободить систему от связанных с этим икажений. В первую очередь это касается массы подвижной системы звукоизлучателя, включающей в себя сумму масс диффузора и катушки. С искажениями данного порядка в усилительной технике достаточно хорошо борется токовый драйвер. Непоятно только почему для компенсации нежелательных процессов, с крайне–выраженными реактивными характеристиками на помощь были призваны линейные приборы, которые с годами очень ощутимо улучшив свою линейность не приблизились к решению проблемы и на половину. Этот подход не имеет абсолютного решения, так как для его реализации потребовалось бы, сократив время задержки обратной связи до неопределённо малых значений, создать ещё и источник питания с запредельным запасом по току. Подобные “решения” всегда вызывали улыбку прагматика. И ведь не мудрено, раз увидев “гроб” от Sonic Frontiers который играючи, сутками напролёт, своим килоВаттом биаса, с лёгкостью прижав на лопатки, хилые, совдеповские счётчики, был готов поиграть на акустике своего обладателя всего четырьмя Ваттами которые в здравом уме, оплатить не согласится никто и никогда.
Muleteer DSP решает задачу доставки требуемого количества энергии в нужное время, не имея при этом недостатков современных решений. Во первых, алгоритм имеет информацию о будущих, пока только запланированных эволюциях. Объединив эти данные с постоянной величиной массы излучателей, требующих контроля, мы получаем возможность воздействия на реактивную систему, абсолютно комплементарно организованной системой, не применяя для этого исключительных и по сути диких мер. Таким образом, хотя бы математически, проблема избыточной массы имеет абсолютное решение. И я надеюсь, что теперь, вы имеете не менее точную, его реализацию.
Download: foo_dsp_muleteer.zip
Примечания:
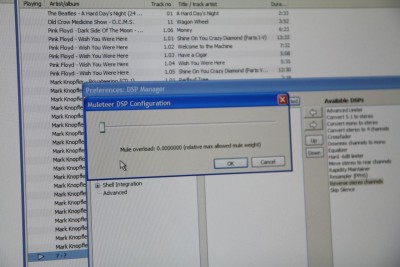
1. Активируйте "Rapidity Maintainer" из списка доступных DSP.
2. Прикиньте перевес вашей системы. Современные системы имеют данное значение в районе 0.5–1.5. Попытайтесь не отклоняться сильно от этих значений. Только счастливые обладатели ламповой техники имеют возможность пробовать значения больше 2.0.
3. Так как Muleteer фунционирует на уровне более точном, чем тот который был выбран инженерами как "достаточный" (возможно неправильно интерпретирующими теорему Котельникова–Шеннона) (*), рекомендуется двух кратный апсемпл для материала CD качества. Просто вставьте ресемплер в цепочку обработки DSP –ДО– модуля Muleteer. Пытайтесь избегать всякого рода дизеринга, такого как "noise shaping" и.т.п. Особенно после модуля Muleteer, так как результат его работы, строго говоря, уже не может считаться PCM.
4. Подстройте модуль до желаемого результата.
5. Наслаждайтесь.
CYa, copah (aka Владимир Копьёв)
mailto: copah@yandex.ru
*) Теорема дискретов Котельникова–Шеннона гласит следующее: «Сигнал с ограниченой полосой может быть абсолютно точно восстановлен при условии использования бесконечно большого количества отсчётов, если, частота дискретизации равна 2-х кратному значению верхней частотной границы полосы».
Заметьте: БЕСКОНЕЧНОЕ количество отсчётов... Простой пример. Возьмём синусоидальный сигнал с частотой F и последовательностью значений [1,-1,1,-1,1,-1,1] при частоте дискретизации 2F. В таком случае, при сдвиге фазы данного сигнала на π/4 радиан мы получим последовательность [0.7,-0.7,0.7,-0.7,0.7,-0.7,0.7]. Но точно такую же последовательность мы получим просто аттеньюировав этот сигнал на 0.7. Этот пример демонстрирует невозможность дескриминации амплитуды и фазы, частоты F на живом (конечном) сигнале. Для Компакт Диска это означает неизбежность ошибок при декодировании, так как никто не пожелает, да и не сможет играть нотами бесконечными по продолжительности. С другой стороны, при частоте дискретизации 4F, сигнал может быть восстановлен с использованием лишь только двух отсчётов (эквивалентных одному отсчёту для 2F), так как первая производная может быть рассчитана до 2F отсчёта с идеальным выравниванием по времени. Таким образом, для частоты дискретизации 2F, полоса 0F — 1/2F свободна от ошибок. А полоса 1/2F — F имеет коэффициент гармоничемких искажений: E'f(t) = f/Fs*t если я правильно считаю… ;-)
Muleteer DSP v0.78
Список разделов › foobar2000 › Плагины
vshaev
Не после а до строка из рекомендации автора Просто вставьте ресемплер в цепочку обработки DSP до модуля Muleteer.
Не после а до строка из рекомендации автора Просто вставьте ресемплер в цепочку обработки DSP до модуля Muleteer.
- freedom1917g
- Репутация: 2
- С нами: 16 лет 6 месяцев
freedom1917g,
Точно, куда я смотрел?
Но мне однозначно звук приятнее при ресемплере ПОСЛЕ плагина
Точно, куда я смотрел?
Но мне однозначно звук приятнее при ресемплере ПОСЛЕ плагина

- vshaev
- Репутация: 1
- С нами: 13 лет 1 месяц
sudden, я не знаком с микролабами. Однако склоняюсь к мнению, что эффект от плагина не перевесит других косяков этой активной акустики. В бюджетном диапазоне неплохо играют активные мониторы Mackie MR5 mkII — я бы сказал это минимальный уровень по качеству, когда использование плагина оправдано. Бывают конечно всякие исключения. Но одни НЧ головы путёвые стоят $500 за пару. Пищалки ещё дороже. Что уж про акустику говорить.
Добавлено спустя 18 минут 28 секунд:
Добавлено спустя 18 минут 28 секунд:
Это не украшалка звука. Правильно настроенный плагин позволяет получить более точный звук, а не более красивый.vladj:Все, кому понравилось звучание с этим плагином, получили очередную улучшалку - украшалку звука.
- copah
- Автор темы

- Откуда: Екатеринбург
- Репутация: 20
- С нами: 12 лет 10 месяцев
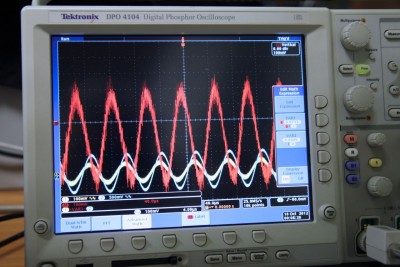
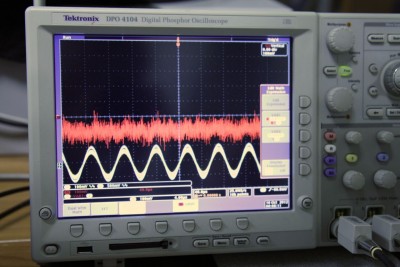
Лабораторные испытания
Плагин не задействован.
Плагин работает.
Добавлено спустя 33 минуты 57 секунд:
Характеристики тестовой установки.
1. Компьютер с ОС Win Vista.
2. foobar2000
3. Модифицированный Muleteer DSP. Модифицирован с целью исключить любое воздействие из правого канала.
3. Осциллограф Tektronix DPO 4104.
3-а. Первым каналом включен в левый канал параллельно с нагрузкой в виде динамического излучателя по типу капсюля от головных телефонов.
3-б. Вторым каналом включен в референсный правый канал находящийся в состоянии отсутствия какой либо нагрузки.
3-в. Мат-канал сконфигурирован выражением (1)*VAR1-(2). VAR1 выставлен опытным путём равным 6.713 для компенсации снижения ЭДС, вызванного активной составляющей нагрузки.
Вот вроде бы и всё. Мат-канал наглядно демонстрирует меру несоответствия ЭДС в нагруженном канале — эталонной. На фото отчётливо видно что коэффициент воздействия 0.83 — оптимален для данной пары драйвера тока и излучателя. Драматизм происходящего вне контроля Muleteer DSP не заслуживает отдельного комментария, поскольку это тот случай, когда лучше один раз увидеть.
- copah
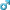
- Автор темы

- Откуда: Екатеринбург
- Репутация: 20
- С нами: 12 лет 10 месяцев
Красиво, но не убедительно. Число пользователей, умеющих пользоватся двухканальным, запоминающим осциллографом и понять суть этик картинок
уничтожающе мало. Лично мне мало, что я слышу разницу в звучании, мне желательно и объяснение доступным языком, что происходит с сигналом при работе плагина. А пока я видел что-то в виде околесицы (сорри). Главное, что мы не имеем никакой обратной связи компьютера с усилителем и акустикой.
То, что вышло из звуковой карты, никак не может влиять на усилитель и акустику. Они сами по себе. Да, у всех они разные, движком плагина мы можем
изменить АЧХ выводимого сигнала и получить звук, удовлетворяющий нас именно на наших усилителе и акустике.
Наверное просто в начале темы не нужно было приплетать в объяснениях понятия ООС, демпфирование, головки и прочие вещи, которые мы имеем
после компьютера. Плагин обрабатывает звук до выхода его из компа, независимо от того, что мы там дальше зацепили.
Я-ж согласился, что звук может и интересней становится, но это для тех, кто любит пользоватся DSP, эквалайзерами и прочими фичами и на выходе
из компа они получают уже не честный, без обработки звук, а приукрашенный по их разумению.
Я с Вами рядом не сидел при этих испытаниях и не видел, какие кнопочки на осциллографе нажимались на нём в каждом случае, где измерялся сигнал
(акустика, усилитель, линейный выход звуковой карты, кстати какая она ?)и откуда он был взят, т.е. источник.
Все напоминания о себе уже бессмысленны, вроде-бы договорились уже, кому понравилось, пользуются, остальные нет. Что изменилось за пару месяцев ?
Вышла новая версия плагина ? Думаю, тут всё проще, нездоровое самолюбование, только и всего. Ажиотажа не будет никогда и нигде, неужели непонятно.
И ещё, если Вы такой "хороший и пушистый", то почему ?
"Download software from Vladimir Kopjov - CD Player
Сайт может угрожать безопасности вашего компьютера или мобильного устройства
Посещение этого сайта может привести к заражению компьютера или мобильного устройства вредоносными программами, использованию его без вашего ведома, а также к порче или краже ваших данных. "
"
PS. По какой причине не отвечали на вопросы пользователей по плагину CD Reader, люди ставили, тащились от звука тоже исключительного плагина. Интересно,
а что там с потоком звуковым с CD можно заделать. Там что, звук не побитово рипался, а с украшениями ?
уничтожающе мало. Лично мне мало, что я слышу разницу в звучании, мне желательно и объяснение доступным языком, что происходит с сигналом при работе плагина. А пока я видел что-то в виде околесицы (сорри). Главное, что мы не имеем никакой обратной связи компьютера с усилителем и акустикой.
То, что вышло из звуковой карты, никак не может влиять на усилитель и акустику. Они сами по себе. Да, у всех они разные, движком плагина мы можем
изменить АЧХ выводимого сигнала и получить звук, удовлетворяющий нас именно на наших усилителе и акустике.
Наверное просто в начале темы не нужно было приплетать в объяснениях понятия ООС, демпфирование, головки и прочие вещи, которые мы имеем
после компьютера. Плагин обрабатывает звук до выхода его из компа, независимо от того, что мы там дальше зацепили.
Я-ж согласился, что звук может и интересней становится, но это для тех, кто любит пользоватся DSP, эквалайзерами и прочими фичами и на выходе
из компа они получают уже не честный, без обработки звук, а приукрашенный по их разумению.
Я с Вами рядом не сидел при этих испытаниях и не видел, какие кнопочки на осциллографе нажимались на нём в каждом случае, где измерялся сигнал
(акустика, усилитель, линейный выход звуковой карты, кстати какая она ?)и откуда он был взят, т.е. источник.
Все напоминания о себе уже бессмысленны, вроде-бы договорились уже, кому понравилось, пользуются, остальные нет. Что изменилось за пару месяцев ?
Вышла новая версия плагина ? Думаю, тут всё проще, нездоровое самолюбование, только и всего. Ажиотажа не будет никогда и нигде, неужели непонятно.
И ещё, если Вы такой "хороший и пушистый", то почему ?
"Download software from Vladimir Kopjov - CD Player
Сайт может угрожать безопасности вашего компьютера или мобильного устройства
Посещение этого сайта может привести к заражению компьютера или мобильного устройства вредоносными программами, использованию его без вашего ведома, а также к порче или краже ваших данных.
 "
"PS. По какой причине не отвечали на вопросы пользователей по плагину CD Reader, люди ставили, тащились от звука тоже исключительного плагина. Интересно,
а что там с потоком звуковым с CD можно заделать. Там что, звук не побитово рипался, а с украшениями ?
- vladj

- Откуда: Пермский край
- Репутация: 427
- С нами: 15 лет 4 месяца
Осциллограф был один раз настроен как было описано выше. Дальше его не касались. Испытания проводила независимая лаборатория. Если вы будете настаивать, я могу попросить высказаться здесь людей их проводивших.vladj:Я с Вами рядом не сидел при этих испытаниях и не видел, какие кнопочки на осциллографе нажимались на нём в каждом случае, где измерялся сигнал
Я не понимаю, как можно отрицать то что уже очевидно ? Вам плохо видно что-ли, что под управлением плагина сигнал близок к эталонному настолько, что ближе уже некуда.vladj:Я-ж согласился, что звук может и интересней становится, но это для тех, кто любит пользоватся DSP
Возможно, меня оскорбляют ваши безапелляционные утверждения о том что я лгу. Я в очередной раз предоставил доказательства истинности сказанного и сделанного мной. Опыт поставлен, специально для вас, наитривиальнейший. Если вы такой ярый "борец" за правду, будьте добры, повторите эксперимент — сравним результаты. А то так, у вас, всё больше как в басне: "собака лает — караван идёт".vladj:Думаю, тут всё проще, нездоровое самолюбование
Давайте ссылку. Это всё раскопировано десятками миллионов копий по интернету. Я не могу за каждую отвечать.vladj:Посещение этого сайта может привести к заражению компьютера
Звук риповался — прямее некуда. Просто при классическом воспроизведении из CD транспорта цифры вылазят далеко не те что на диске записаны.vladj:Там что, звук не побитово рипался, а с украшениями ?
- copah
- Автор темы

- Откуда: Екатеринбург
- Репутация: 20
- С нами: 12 лет 10 месяцев
Поддерживаю vladj! Странно Вы copah, отвечаеете на вопросы...), по сути просто ничего..., в основном..., то что цепляет в большей степени Ваше самолюбие...)vladj:−
Сообщение vladj » Вчера, 23:03
Красиво, но не убедительно. Число пользователей, умеющих пользоватся двухканальным, запоминающим осциллографом и понять суть этик картинок
уничтожающе мало. Лично мне мало, что я слышу разницу в звучании, мне желательно и объяснение доступным языком, что происходит с сигналом при работе плагина. А пока я видел что-то в виде околесицы (сорри). Главное, что мы не имеем никакой обратной связи компьютера с усилителем и акустикой.
То, что вышло из звуковой карты, никак не может влиять на усилитель и акустику. Они сами по себе. Да, у всех они разные, движком плагина мы можем
изменить АЧХ выводимого сигнала....
p.s
а вообще Ваш плагин нужен, для не здоровых аудиофилов зашедших в тупик, от поиска своего звука..., он как таблетка снять симптом болезни на неделю.
- foo_val

- Репутация: 12
- С нами: 15 лет 3 месяца
vladj:Главное, что мы не имеем никакой обратной связи компьютера с усилителем и акустикой.
То, что вышло из звуковой карты, никак не может влиять на усилитель и акустику. Они сами по себе
Да, конечно, но отсутствие ОС -это не всегда смертельно. При условии, что ты четко знаешь, что тебе там, в дальнейшем тракте, нужно откорректировать и при том, что то, дальнейшее, ведет себя одинаковым образом. Т.е., грубо говоря, стоит у тебя за звуковой картой паразитный резистивный делитель на 2, который тебе не нужен, и ты, не имея с него обратной связи, просто поднимаешь выходной сигнал на 6 дБ, нивелируя воздействие делителя. Или, например, дальше по тракту висит операционник с двойным Т-мостом или мостом Вина в петле ОС. Знаешь, что будет ненужный резонанс, можешь заранее его зеркально откорректировать. Т.е. коррекция не по сигналу обратной связи, а по прогнозу. И более-менее точной/грубой настройкой этого прогноза. Другое дело, что уши - не лучший датчик точности настройки обратной коррекции, что непонятно, на какой частотный диапазон эта коррекция распространяется, что будет в случае с 2-х - 3-хполосной АС, у которой резонансные частоты, массы соколеблющегося воздуха разные у каждого из динамиков, ну, и много чего еще непонятно. А у автора нет желания внятно объяснять, поэтому что тут обсуждать...
- onv
- Откуда: Харьков
- Репутация: 52
- С нами: 13 лет 1 месяц
Тут подробней пож-та, что им мешает вылазить как нужно и как Ваш CD риппер помогает в этом.copah:классическом воспроизведении из CD транспорта цифры вылазят далеко не те что на диске записаны
Вообще, я думал что eac нормально рипает, ан нет, ему мешает что-то побитово музыку выгнать.
Получается без ваших наработок никак ? Ни музыку с CD послушать, ибо она криво выходит с привода,
ни скачанную толком послушать, ибо без Вашего плагина фиг знает, что творится с усилком, акустикой и проч.
Надоело мне тут с Вами препиратся, может кто найдётся из "благодарных", вот пусть они и льют Вам елей по самое не хочу.
- vladj

- Откуда: Пермский край
- Репутация: 427
- С нами: 15 лет 4 месяца
foo_val, Это вы это вопросом называете ?
Могу лишь гадая, что вы там имели ввиду ответить. Следует понимать, то что все элементы системы перечисленные выше влияют в первую очередь на звук. И в этом смысле справедливо рассматривать каждый из них как фильтр имеющий свою уникальную импульсную характеристику. Тогда звуковой спектр будет равен сумме спектров фильтров (компонент) системы. Поскольку сумма спектров равна спектру суммы то все названые компоненты имеют одинаковые возможности по влиянию на звук. Так что уличить во лжи я вас не могу. Потому как то что вы там наплели, это самая что ни на есть патологическая ахинея.
А вы не стесняйтесь задавать их! А то я до сих пор ни одного внятного вопроса по сути ни от вас ни от вас не услышал. Вы лишь только с уверенностью Алана Чумака рассказываете, как устроен сконструированный мной фильтр, каково моё здоровье и чем я завтракал вчера и завтра. И давайте договоримся, если вы и правда захотите задать мне вопросы, будем их нумеровать (1. 2. 3. или а. б. в. как угодно) и в конце ставить знак вопроса, чтобы мне не приходилось догадываться чего вы хотите. Вопрос задать, или на жизнь пожаловаться. А я буду давать вам ответов по количеству цифр там или букв. Это я могу обещать.
У вас есть конструктивные замечания по сути эксперимента ?
Да остановитесь вы уже. Хватит гадать. Хватит врать тут о том как работает мой фильтр. Или потрудитесь тут объяснить какие измерения позволяют вам говорить о том как он устроен внутри. А то уже вопрос начинает одолевать один... Вы хоть раз в жизни, кинули на вентилятор, что нибудь, кроме него ?
Добавлено спустя 8 минут:
onv, да задайте же вы свой вопрос наконец !!! Хотя вообще-то у меня складывается впечатление, что вам и так всё ясно. По крайней мере, всё о чём вы только-что писали имеет место быть.
Добавлено спустя 3 минуты 28 секунд:
Добавлено спустя 4 минуты 23 секунды:
Дак вот как вы сами же и любите выражаться с vladj, это лепет какой-то. Что вышло ? Напряжение ? Ток ? Вчерашний обед ? Влиять наверное и вправду не может не на усилитель не на акустику, ну и что ? В чём суть вопроса то ? Как на такое отвечать ?vladj:То, что вышло из звуковой карты, никак не может влиять на усилитель и акустику. Они сами по себе.
Могу лишь гадая, что вы там имели ввиду ответить. Следует понимать, то что все элементы системы перечисленные выше влияют в первую очередь на звук. И в этом смысле справедливо рассматривать каждый из них как фильтр имеющий свою уникальную импульсную характеристику. Тогда звуковой спектр будет равен сумме спектров фильтров (компонент) системы. Поскольку сумма спектров равна спектру суммы то все названые компоненты имеют одинаковые возможности по влиянию на звук. Так что уличить во лжи я вас не могу. Потому как то что вы там наплели, это самая что ни на есть патологическая ахинея.
foo_val:Странно Вы copah, отвечаеете на вопросы
А вы не стесняйтесь задавать их! А то я до сих пор ни одного внятного вопроса по сути ни от вас ни от вас не услышал. Вы лишь только с уверенностью Алана Чумака рассказываете, как устроен сконструированный мной фильтр, каково моё здоровье и чем я завтракал вчера и завтра. И давайте договоримся, если вы и правда захотите задать мне вопросы, будем их нумеровать (1. 2. 3. или а. б. в. как угодно) и в конце ставить знак вопроса, чтобы мне не приходилось догадываться чего вы хотите. Вопрос задать, или на жизнь пожаловаться. А я буду давать вам ответов по количеству цифр там или букв. Это я могу обещать.
foo_val:Поддерживаю vladj!
У вас есть конструктивные замечания по сути эксперимента ?
vladj:движком плагина мы можем изменить АЧХ
Да остановитесь вы уже. Хватит гадать. Хватит врать тут о том как работает мой фильтр. Или потрудитесь тут объяснить какие измерения позволяют вам говорить о том как он устроен внутри. А то уже вопрос начинает одолевать один... Вы хоть раз в жизни, кинули на вентилятор, что нибудь, кроме него ?
Добавлено спустя 8 минут:
onv, да задайте же вы свой вопрос наконец !!! Хотя вообще-то у меня складывается впечатление, что вам и так всё ясно. По крайней мере, всё о чём вы только-что писали имеет место быть.
Добавлено спустя 3 минуты 28 секунд:
EAC это делает лучше всех. Но причём здесь он ? Вы вообще читаете что вам пишут ?vladj:Вообще, я думал что eac нормально рипает
Добавлено спустя 4 минуты 23 секунды:
Всё зависит от степени влияния коррекции. Уши порой точнее многого другого. На слух я плагин настроил на 0.7-0.75 а по диф-системе визуально вышло 0.82 так-что тут грех жаловаться.onv:Другое дело, что уши - не лучший датчик точности настройки обратной коррекции
- copah
- Автор темы

- Откуда: Екатеринбург
- Репутация: 20
- С нами: 12 лет 10 месяцев
Косвенно о многополосных АС я вопрос уже задал. В общих чертах действительно, догадываюсь. Еще с тех пор, когда я ходил под стол пешком, ко мне под этот стол периодически наезжала редакция журнала "Радио", потом мои радиоинженеры работали в редколлегии у Николая Сухова. Теорему Котельникова от дросселя с трудом, но отличаю.copah:onv, да задайте же вы свой вопрос наконец !!! Хотя вообще-то у меня складывается впечатление, что вам и так всё ясно.
- onv
- Откуда: Харьков
- Репутация: 52
- С нами: 13 лет 1 месяц
copah, нисколько не хочу критиковать ваш труд. Единственное, с чем я хочу согласиться — толком не понятно что именно делает этот фильтр. К сожалению, инженеры не всегда умеют выражать мысль так, чтобы её понял неподготовленный читатель. Сам с этим в себе борюсь иногда :)
Посмотрите, как просто и понятно Chris Montgomery (автор Ogg Vorbis) вводит в курс дела неподготовленного читателя: A Digital Media Primer for Geeks (там есть русские субтитры). Попробуйте так же просто объяснить суть вашего фильтра для читателя, который посмотрел этот ролик и не слишком разбирается в вашей профессиональной терминологии. Просто кратко введите в курс дела. Потом на основе этих материалов может получиться хорошая статья, которая будет сопровождать ваш плагин.
Посмотрите, как просто и понятно Chris Montgomery (автор Ogg Vorbis) вводит в курс дела неподготовленного читателя: A Digital Media Primer for Geeks (там есть русские субтитры). Попробуйте так же просто объяснить суть вашего фильтра для читателя, который посмотрел этот ролик и не слишком разбирается в вашей профессиональной терминологии. Просто кратко введите в курс дела. Потом на основе этих материалов может получиться хорошая статья, которая будет сопровождать ваш плагин.
- VEG
- Администратор

- Откуда: Finland
- Репутация: 279
- С нами: 13 лет 1 месяц
onv, Много-полосные АС по хорошему требуют расширения мат-модели. Я конечно же это понимаю. Но мне интуитивно кажется, что разница не будет большой. Дело в том что мера воздействия массы на колебательную систему прямо-пропорционально частоте на которой оно происходит. Тоесть основная масса искажений рождается в пищалке. Потом однако я понял что у средне-частотника удельная масса может быть намного больше массы пищали. Вполне настолько больше чтобы нивелировать снижение частоты массой. Тоесть безусловно, АС, особенно 3-х полосные, и более требуют собственной модели. Всё это не особо сложно добавить, только мне пока отлаживать не на чем. И потом там такая гацкая штука есть внутри — кросс-овер. Надо тоже его попросчитывать — получится ли избежать его параметризации... Потому как если нет то настроить (в смысле подобрать в мат-модель коэффициенты) такое дома будет просто невозможно. Вообще у меня есть мнение что многие производители АС используют кроссоверы для коррекции завалов в АЧХ, подгонкой резонанса в области провалов. На таких вообще ничо работать нормально не будет никогда.
Добавлено спустя 5 минут 12 секунд:
Вообще для трёх-полосника даже минимальная параметризация выглядит устрашающе. Три массовых коэффициента, два значения границ частот, и плюс две величины порядка фильтров. Как-то мне кажется даже это уже обычному человеку ну никак не настроить.
Добавлено спустя 16 минут 12 секунд:
VEG, суть проблемы в том что из за разности масс, диафрагма не согласована со средой на 100%. Пропорционально отношению масс часть энергии излучается а часть задерживается на время "в массе", потом напрямую участвуя в создании нелинейных искажений. Задача постоянно и как можно оперативней компенсировать избыточный момент силы.
Не знаю задавайте наводящие вопросы, что конкретно не ясно... ?
Добавлено спустя 5 минут 12 секунд:
Вообще для трёх-полосника даже минимальная параметризация выглядит устрашающе. Три массовых коэффициента, два значения границ частот, и плюс две величины порядка фильтров. Как-то мне кажется даже это уже обычному человеку ну никак не настроить.
Добавлено спустя 16 минут 12 секунд:
VEG, суть проблемы в том что из за разности масс, диафрагма не согласована со средой на 100%. Пропорционально отношению масс часть энергии излучается а часть задерживается на время "в массе", потом напрямую участвуя в создании нелинейных искажений. Задача постоянно и как можно оперативней компенсировать избыточный момент силы.
Не знаю задавайте наводящие вопросы, что конкретно не ясно... ?
- copah
- Автор темы

- Откуда: Екатеринбург
- Репутация: 20
- С нами: 12 лет 10 месяцев
Это понятно. Конечно используют, это дешево и сердито. Поэтому чисто логически и просится в N-полосной АС эксперимент по разбивке на n диапазонов с автономными внутри полосы настройками, которые будут работать в диапазоне, не заползающем на зону раздела фильтров, по крайней мере, например, по -3дБ в обе стороны от каждого кроссовера просто не обрабатывать. А вот учитывать частоты механического резонанса и добротность хотя бы головок, без учета акустического оформления, и того, насколько оно резонансы сдвигает (это без измерительных микрофонов никто дома не посчитает) и вводить антикоррекцию соответствующую, наверное, было бы нелишним.copah:И потом там такая гацкая штука есть внутри — кросс-овер. Надо тоже его попросчитывать — получится ли избежать его параметризации... Потому как если нет то настроить (в смысле подобрать в мат-модель коэффициенты) такое дома будет просто невозможно. Вообще у меня есть мнение что многие производители АС используют кроссоверы для коррекции завалов в АЧХ, подгонкой резонанса в области провалов. На таких вообще ничо работать нормально не будет никогда.
P.S. Вплоть до того, что, если не успеваем отрабатывать сразу 3 полосы, или, банально, например, не знаем ни частот раздела, ни порядка фильтров, ни что за головы стоят 2-х полосах из 3-х, оставлять включенной в обработку только известную полосу, на остальное забить.
Последний раз редактировалось onv 17.10.2012, 03:53, всего редактировалось 1 раз.
- onv
- Откуда: Харьков
- Репутация: 52
- С нами: 13 лет 1 месяц
Я бы не стал так осторожничать, сказав, что присутствие OOC смертельно почти всегда.onv:Да, конечно, но отсутствие ОС -это не всегда смертельно.
Добавлено спустя 22 минуты 26 секунд:
onv, Ну хорошо, давайте я возьму пару недель подумать о уровне возможно-допустимой оптимизации подобной системы. А там посмотрим... И потом вы первый выразивший подобное желание. Подумайте..., какого типа АС интересны в первую очередь ? Думаю проще начинать с тряпичных типа Dynaudio или Dali. Насчёт металлических типа Monitor и B&W мне кажется 50-50 что кина не будет.
Добавлено спустя 12 минут 19 секунд:
По сравнению с лишней массой это капелюшка в море. Вот просто смело можно сократить. Ну сколько может паук тянуть ??? Да хоть килограмм. Возьмите ну не знаю грамм 15 диффузор и посчитайте каким моментом он будет обладать при пересечении нейтрали на частоте 10 kHz с амплитудой в 5 см... А если ещё катушку разомкнуть в этот момент... потом посчитаю для интереса но что-то кажется мне, было бы пауков даже 10, никто б и не понял что они были.onv:А вот учитывать частоты механического резонанса и добротность хотя бы головок
Добавлено спустя 25 минут 13 секунд:
в данной реализации одна масса во всём диапазоне. Математика очень точная, поэтому не хотелось чем-то ещё портить.onv:непонятно, на какой частотный диапазон эта коррекция распространяется
Добавлено спустя 1 минуту 21 секунду:
для головных телефонов — лучший вариант.
- copah
- Автор темы

- Откуда: Екатеринбург
- Репутация: 20
- С нами: 12 лет 10 месяцев
И это понятно. А стоит ли овчинка выделки, должен, по идее, сразу показать тот же осцилл. Подключить один твиттер с ФНЧ, без ничего, это и будет аналог ушей, настроиться коэффициентом под него, убрать, подставить тарелку под тот же коэффициент и смотреть результат. Если разбег в коэффициентах неприличный, значит, стОит.copah:для головных телефонов — лучший вариант.
- onv
- Откуда: Харьков
- Репутация: 52
- С нами: 13 лет 1 месяц
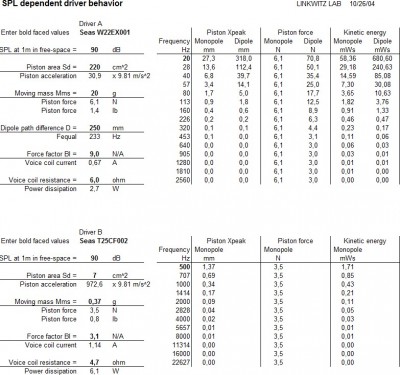
onv, посчитал я тут маленько. Двухполосник на Scan-Speak Audio Technology — никакого резону...
Scan Speak Discovery: mm=0.33g D=1" S=0.785sq.in mm/S=2.378
Audio Technology Flex: mm=37g D=10" S=78.5sq.in mm/S=2.121
И это разные брэнды... Хоть и куратор один. Я сдесь вижу очередное подтверждение того что скажем в Dynaudio очень хорошо понимают, что делают. Копнуть бы данные по другим головам... Но уже видно, что хотя бы на порядок тут уже не наковырять.
Я конечно предполагал нечто подобное... Но каково ? Тютелька в тютельку подогнано. Рискну даже спрогнозировать, что удельный 2.3 стандарт для всех бошек Скаанинга. А может даже и у большей массы производителей он тот же.
Добавлено спустя 12 минут 31 секунду:
onv, хороший кейс наглядно всё и просто очень. Могу однако даже поспорить с теми головами что я прикидку делал, коэффициент будет одинаковый.
А вы вообще так-то пускали на акустике эту хрень ? А то я сам так ни разу и несподобился.
Добавлено спустя 6 минут 54 секунды:
В общем моё мнение нету в усложнении смысла никакого. Чо там тарелка уже на 2K не играет. А ниже ООС отлично справляется. Да даже без неё в районе 2K КНИ меньше на порядок а то и на два чем на 20-и...
Scan Speak Discovery: mm=0.33g D=1" S=0.785sq.in mm/S=2.378
Audio Technology Flex: mm=37g D=10" S=78.5sq.in mm/S=2.121
И это разные брэнды... Хоть и куратор один. Я сдесь вижу очередное подтверждение того что скажем в Dynaudio очень хорошо понимают, что делают. Копнуть бы данные по другим головам... Но уже видно, что хотя бы на порядок тут уже не наковырять.
Я конечно предполагал нечто подобное... Но каково ? Тютелька в тютельку подогнано. Рискну даже спрогнозировать, что удельный 2.3 стандарт для всех бошек Скаанинга. А может даже и у большей массы производителей он тот же.
Добавлено спустя 12 минут 31 секунду:
onv, хороший кейс наглядно всё и просто очень. Могу однако даже поспорить с теми головами что я прикидку делал, коэффициент будет одинаковый.
А вы вообще так-то пускали на акустике эту хрень ? А то я сам так ни разу и несподобился.
Добавлено спустя 6 минут 54 секунды:
В общем моё мнение нету в усложнении смысла никакого. Чо там тарелка уже на 2K не играет. А ниже ООС отлично справляется. Да даже без неё в районе 2K КНИ меньше на порядок а то и на два чем на 20-и...
- copah
- Автор темы

- Откуда: Екатеринбург
- Репутация: 20
- С нами: 12 лет 10 месяцев
Да, у Dynaudio культура высока, безусловно. Мой друг остановился на contour 1.1, но мне мои больше нравятся. Можно попробовать Зигфриду Линквицу в лоб задать вопрос, как у него в orion-ах и pluto обстоит с равенством удельных, если в нем инженер преобладает над бизнесменом, есть шанс, что ответит.copah:И это разные брэнды... Хоть и куратор один. Я сдесь вижу очередное подтверждение того что скажем в Dynaudio очень хорошо понимают, что делают. Копнуть бы данные по другим головам... Но уже видно, что хотя бы на порядок тут уже не наковырять.
Это о чем ?copah:onv, хороший кейс наглядно всё и просто очень. Могу однако даже поспорить с теми головами что я прикидку делал, коэффициент будет одинаковый.
Возможно. Тарелки бывают и в среднечастотном звене, так что я бы говорил о 5кГц. "Эту хрень" на акустике отслушаю на выходных.copah:В общем моё мнение нету в усложнении смысла никакого. Чо там тарелка уже на 2K не играет.
Добавлено спустя 5 часов 30 минут 22 секунды:
copah:Копнуть бы данные по другим головам...
Здесь кое-что есть (~ 5000)
http://www.41hz.com/forums/content.php?253-TSdb
- onv
- Откуда: Харьков
- Репутация: 52
- С нами: 13 лет 1 месяц
onv:Это о чем ?
onv:Подключить один твиттер с ФНЧ, без ничего
Буду ждать, у меня пока никакой нет возможности отслушать акустику. Может и повезёт конечно, возможно с 1.1 детёныш не успел разделаться до конца ;-) И электролит из Ревокса не успел весь слиться :-)onv:"Эту хрень" на акустике отслушаю на выходных.
- copah
- Автор темы

- Откуда: Екатеринбург
- Репутация: 20
- С нами: 12 лет 10 месяцев
Только для этого предварительно нужно успеть воткнуть в фубаровскую сборку триггерную кнопку, оперативно переключающую пресеты, и зацепить на нее пультовый хоткей. Без быстрого переключения туда-сюда в реалтайме мелких блох не поймать, метаться к компу и и дергать через сетап бессмысленно, слуховая память успеет потерять мелкие нюансы. И еще было бы очень желательно с того же пульта двигать ползунок плагина. Этот ползунок что-нибудь поддерживает (глобальные Left, Right, например) ? Или, если нет, мне нужно знать, как уверенно поднять окно настроек плагина (имя окна, Class, ClassNN, ID...), передать в него фокус и отдать ползунку пару команд на инкремент/декремент с того же пульта. Желательно хоткеями, чтобы не городить анализ мышиных эвентов.
Добавлено спустя 5 часов 18 минут 58 секунд:
В принципе, по
WinActivate ( "Muleteer DSP Configuration")
ControlFocus ("Muleteer DSP Configuration", "","[CLASS:msctls_trackbar32; INSTANCE:1]")
Send ( "{RIGHT}",0 )
я до ползунка достучался, шевелится с шагом 0,01
Добавлено спустя 5 часов 18 минут 58 секунд:
В принципе, по
WinActivate ( "Muleteer DSP Configuration")
ControlFocus ("Muleteer DSP Configuration", "","[CLASS:msctls_trackbar32; INSTANCE:1]")
Send ( "{RIGHT}",0 )
я до ползунка достучался, шевелится с шагом 0,01
- onv
- Откуда: Харьков
- Репутация: 52
- С нами: 13 лет 1 месяц